O equilíbrio e a beleza na proporção áurea

“Creio que é possível aperfeiçoar uma arte sobretudo a partir de uma base matemática de pensamento”

Max Bill

A Proporção Áurea já mostrou, ao longo da história, ter evidente preferência cognitiva dos seres humanos. “Alguns dos mais antigos indícios de emprego de um rectângulo áureo - ou seja, aquele no qual há uma proporção de 1:1, 618 entre os lados – estão na estrutura de Stonehenge, erguida entre 2450 e 1600 a.C.” (ELAM:2010).

Stonehenge I Fonte: ahduvido.com.br

“A geometria é a linguagem do homem. Mas ao determinar as distâncias respectivas dos objectos, ele inventou ritmos, ritmos sensíveis ao olho, nítidos das suas relações. E esses ritmos estão no nascimento de comportamentos humanos. Ressoam no homem por uma fatalidade orgânica, a mesma fatalidade que faz com “que as crianças, os velhos, os selvagens, os letrados tracem a secção áurea” - Le Corbusier

É possível que a Divina Proporção esteja a ser usada há pelo menos 4.000 anos. Pode ser observada em vários campos de conhecimento, e por anos, cientistas, inventores e curiosos mostraram como ela é a base da beleza e do equilíbrio das formas (e não só). Pitágoras (569 – 500 a.C.), filósofo grego, acreditava que a ordem e a harmonia na natureza teriam explicação na ciência dos números. Gustav Fechner, um psicólogo alemão, intrigado pela secção áurea, realizou um estudo com seres humanos, no final do século XIX, nesse estudo Fechner concluiu que a maior parte das pessoas tinham preferência com os rectângulos cuja a razão média estava próxima de 1:1,618. Este estudo tomou como base milhares de objectos rectangulares, entre eles; livros, caixas, edifícios, jornais. Em 1908 Charles Laio repetiu o mesmo estudo, com maior rigor científico e obteve resultados similares.

“O rectângulo cujos lados adjacentes têm comprimentos em razão que aproxima – se ou é exactamente igual a Φ:1 parece proporcionar uma medida maior de satisfação para um número maior de pessoas que os rectângulos de proporções diferentes” (Huntley, 1985, p. 57)

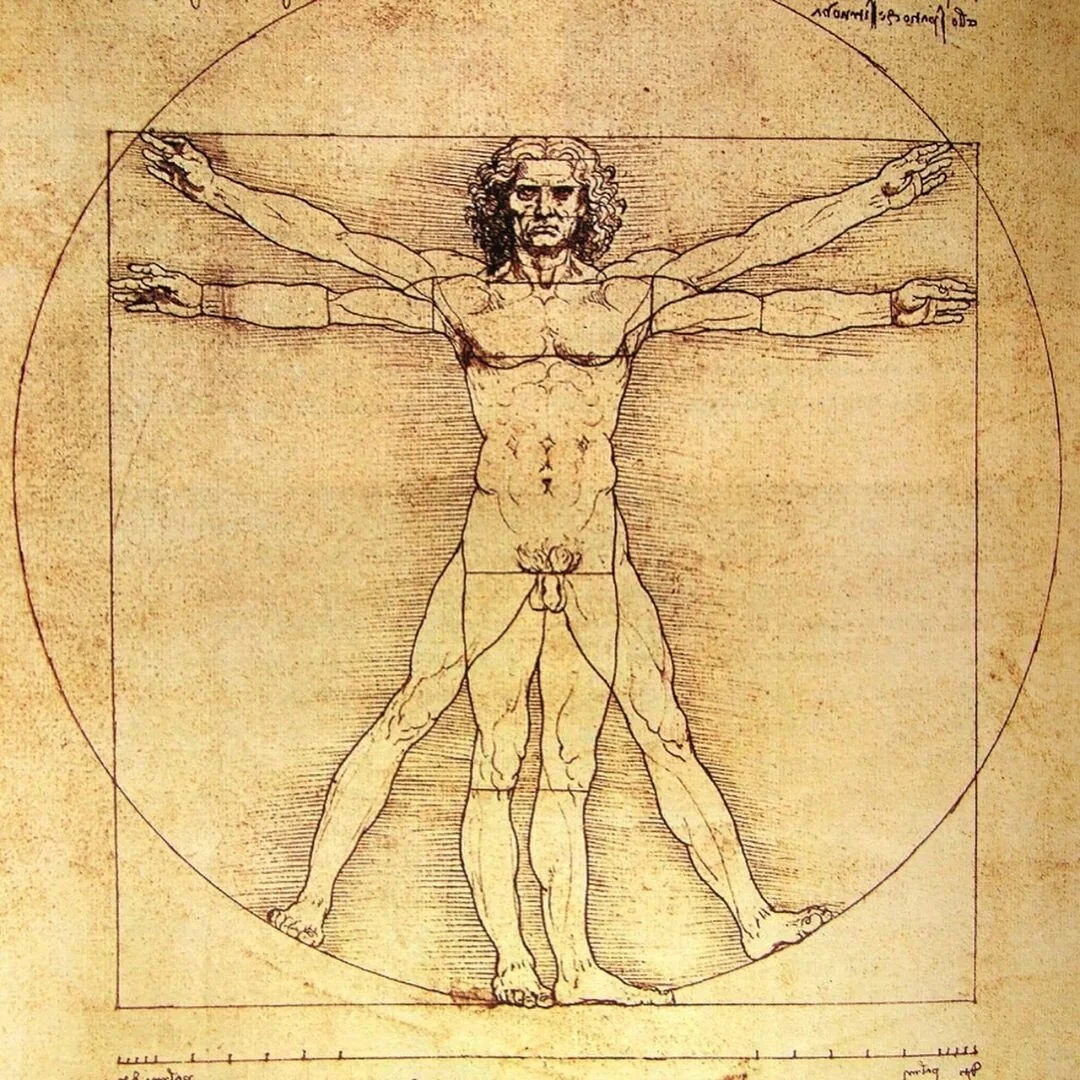
Leonardo da Vinci acreditava que, no Homem perfeito, as dimensões obedecem a proporção áurea e aplicou esses conhecimentos também no conhecido “Homem Vitruviano”.

Homem Vitruviano

“É uma pena que a divisão áurea tenha atraído a entusiástica atenção dos excêntricos. Um deles mediu as alturas de 65 mulheres e comparou os resultados com as alturas de seus respectivos umbigos, tendo obtido a média de 1, 618.” (Huntley, 1985, p. 37)

Outros estudos mostraram que:

a) A proporção de abelhas fêmeas em comparação com abelhas machos numa colmeia é de 1,618.

b) A proporção que aumenta o tamanho das espirais de um caracol é de 1,618.

c) A proporção em que aumenta o diâmetro das espirais sementes de um girassol é de 1,618.

d) A proporção em que diminuem as folhas de uma árvore à medida que subimos é de 1,618.

e) As estrelas distribuem-se perante um astro principal numa espiral obedecendo à proporção de 1,618.

A letra grega da Razão Áurea (Φ)

A letra grega que designa a Razão Áurea é Fi (Φ), letra inicial de Fídias, um importante escultor grego, autor de umas das mais conhecidas estátuas da antiguidade; a Atena Partenos e o Zeus Olímpico. “Em 1509 foi publicado um tratado de Luca Pacioli, De Divina Proportione, ilustrado por Leonardo da Vinci. Reproduzido em 1956 em uma vistosa edição, é um compêndio fascinante da aparição do fi em várias figuras sólidas.” HUNTLEY (1985: 37) O Fi corresponde, aproximadamente a 1, 618. Os egípcios, também usaram esses conhecimentos nas suas construções, especialmente nas pirâmides; as pedras usadas em suas construções seguiam uma proporção constante, cada pedra era 1, 618 menor do que a pedra que estivesse a baixo. Usaram esses conhecimentos, também em templos e sepulcros, pois acreditavam que se assim não fosse, seus deuses não iriam gostar e as almas dos mortos não seguiria o seu destino.

A Sequência de Fibonacci (Fi-Bonacci)

A Sequência de Fibonacci resume-se na lei de que: cada termo é resultado da soma dos dois anteriores. A razão entre o termo posterior com um termo anterior resulta num valor próximo ao número de ouro, ou como já referido acima, Razão Áurea (Φ).

Leonardo Fibonacci (1180 – 1250) procurou explicar a reprodução de coelhos, através de uma sequência que mantinha uma proporção; “Um casal de coelhos atinge a maturidade sexual em dois meses, a cada mês, um casal com maturidade sexual gera um novo casal. Considerando que as condições desses coelhos sejam iguais e ignorando qualquer problema genético, quantos coelhos teremos em N meses?

A resposta é dada pela sequência, considerando cada mês a quantidade de casais, 1,1,2,3,5,8,13,21,34,55,…

Dada pela fórmula: Fn = Fn-1 + Fn – 2.

3/2 = 1,5 ; 5/3 = 1, 666… ; 8/5 = 1, 6 ; 13/8 = 1, 625 ; 21/13 = 1, 615…

O Rectângulo de Ouro

O rectângulo cujos comprimentos AB:AD = Φ é chamado de rectângulo de ouro ou rectângulo áureo, também conhecido como uma espécie de “fonte de prazer”, por apresentar-se mais harmónico e familiar do que os outros. O Partenon, em Atenas, no século V a.C., a célebre obra “A Última Ceia”, de Leonardo da Vinci, são exemplos conhecidos e que se encaixam com perfeição no rectângulo áureo.

Rectângulo de Ouro

Partenon, Atenas I Fonte: www.archdaily.com.br

A Espiral de Ouro

Uma das mais harmónicas curvas, conhecidas em geometria é a espiral de ouro, também designada espiral logarítmica ou espiral equiangular, um símbolo da estética e beleza. Na natureza é possível observar como as câmaras sucessivas da concha de náutilo (frontispício) tem estrutura sobre uma espiral logarítmica.

Corte transversal na concha do Nautilus I Fonte: artsandculture.google.com

Considerações finais

A Proporção Áurea é uma das mais interessentes ferramenta de que dispomos hoje, e, acredito que o importante, em todos os campos, mas com maior ênfase no campo design, é que sua aplicação seja cada vez mais lúcida, consciente e não uma procura de encaixotar uma forma dentro de um rectângulo (por exemplo) apenas para convencer uma audiência, mas para se encontrar a real beleza, o equilíbrio, a funcionalidade necessária.

Estou firme que pouco importa ao cliente ou a quem quer que seja que vai receber ou assistir a apresentação ou receber a proposta, se o designer usou ou não este conhecimento. A este importa o resultado, importa ver se a solução funciona e responde aos requisitos estéticos ou não. Ter o conhecimento das proporções certas e já comprovadas por vários estudos é indispensável para trabalhar no sentido de criar soluções mais harmónicas, mas, uma vez mais, isso precisa ser e parecer natural, feito de forma consciente, para que, de facto, os segredos da matemática, da geometria presentes na Divina Proporção sejam um grande trunfo para os designers que procuram por um equilíbrio entre o que funciona e o que é ao olho humano, belo.

Referências:

ELAM, Kimberly, Geometria do design: estudos sobre proporção e composição, Cosaic Naify, São Paulo, 2010

HUNTLEY, H.E., A Divina Proporção: Um Ensaio Sobre a Beleza na Matemática, S.E., Editora Universidade de Brasília, 1985

TINGA, M.J. Estratégias Persuasivas Aplicadas na Concepção Visual de Cartaz Publicitário. Trabalho de Conclusão de Curso. Universidade Pedagógica. 2017. 140p.